Understanding Exceedance Probability (EP) Curves in Catastrophe Modeling
In the field of catastrophe risk modeling, understanding potential financial impacts from rare, high-severity events is essential for insurers, reinsurers, and risk managers
by Marco Lo Giudice, Head of catastrophe Modeling
In the field of catastrophe risk modeling, understanding potential financial impacts from rare, high-severity events is essential for insurers, reinsurers, and risk managers. One of the most valuable tools for visualizing and interpreting this risk is the Exceedance Probability (EP) curve. This curve is widely used across the insurance and reinsurance industry to quantify and manage potential losses. In this article, we’ll dive into the components of EP curves, what they reveal about risk exposure, and how they empower insurers to make informed decisions in the face of catastrophic events.
What is an EP Curve?
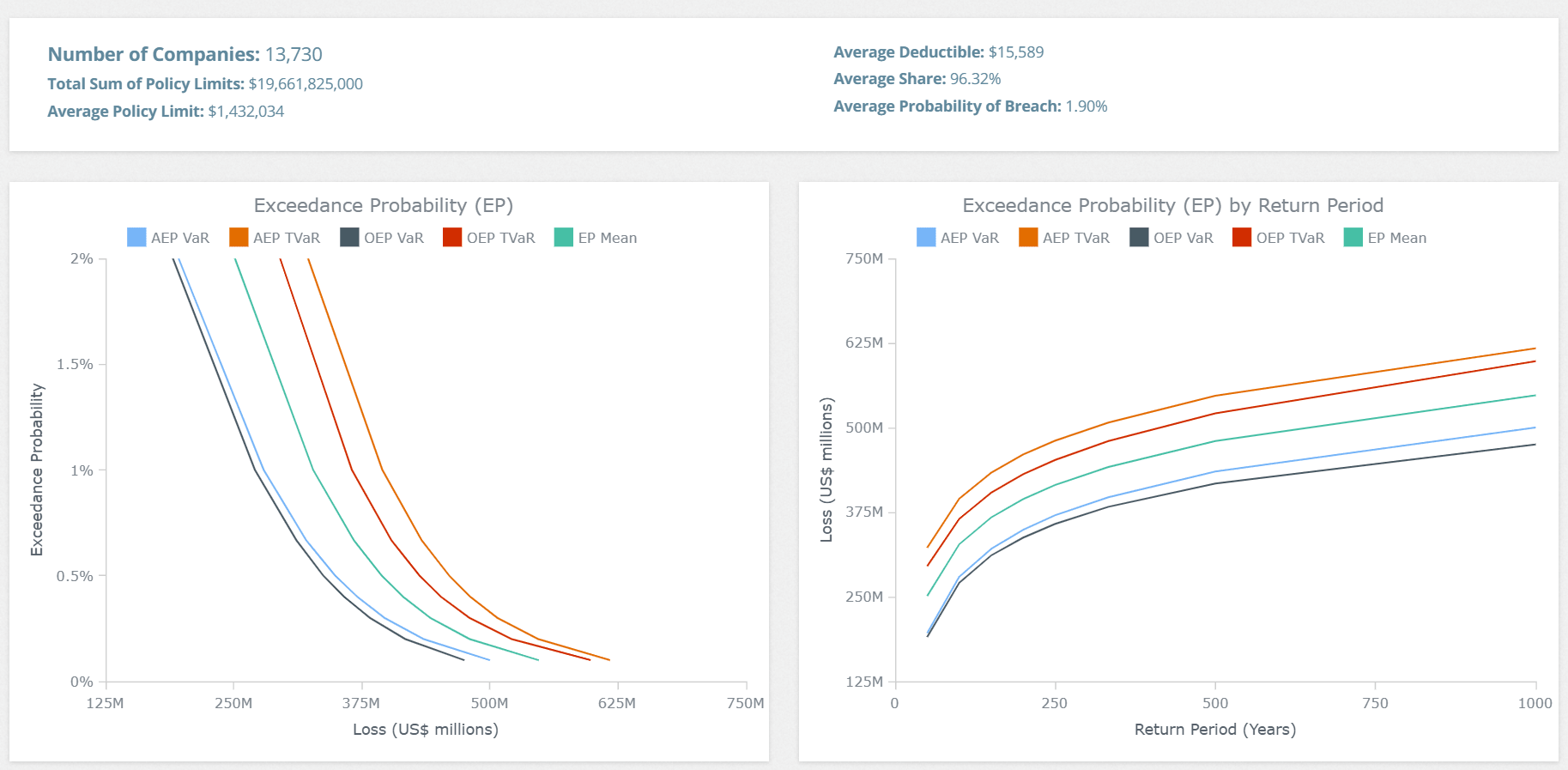
An EP (Exceedance Probability) curve provides a visual representation of the probability that losses will exceed various thresholds within a defined period, such as a year. The curve answers the fundamental question: “What is the likelihood that a certain loss level will be exceeded?”
In the chart, the X-axis represents loss values (often measured in millions of dollars), while the Y-axis shows the probability that the specified loss threshold will be exceeded in a given time frame. The curves provide a quick snapshot of both frequent, lower-severity losses and rare, high-severity losses, allowing stakeholders to gauge the impact of different types of events.
Key Metrics: AEP and OEP, VaR and TVaR
EP curves are often broken down into two types of probabilities—AEP (Aggregate Exceedance Probability) and OEP (Occurrence Exceedance Probability)—and two measures of risk exposure—VaR (Value at Risk) and TVaR (Tail Value at Risk). Let’s explore each in detail:
- Aggregate Exceedance Probability (AEP):
AEP reflects the probability that the total losses from multiple events in a specified time frame (such as a year) will exceed a given threshold. This metric is particularly useful when assessing the cumulative impact of events over a period. Insurers use AEP to understand the total exposure they might face, factoring in multiple occurrences. - Occurrence Exceedance Probability (OEP):
In contrast to AEP, OEP measures the probability that a single event will produce losses above a specified threshold. OEP is essential for evaluating the risk associated with individual, high-impact events. For example, a hurricane or cyberattack that causes a substantial single-event loss would be assessed using OEP. - Value at Risk (VaR):
VaR represents the maximum loss expected at a specified probability level. For instance, if the VaR at the 1% probability level is $1 million, there’s a 1% chance that losses will exceed $1 million in a given period. VaR is a standard metric in risk management, providing a threshold for potential losses. - Tail Value at Risk (TVaR):
TVaR, also known as Conditional Value at Risk, goes a step beyond VaR by calculating the average loss for scenarios where the loss exceeds the VaR threshold. Essentially, TVaR considers “tail risk,” focusing on extreme outcomes. It’s particularly valuable in catastrophe modeling, where rare but severe events can dramatically impact an insurer’s financial standing.
How to Interpret an EP Curve
In an EP curve graph, you’ll typically see separate lines representing AEP and OEP, along with distinct curves for VaR and TVaR for each. Here’s what each curve means in practical terms:
- AEP VaR and AEP TVaR: These curves show the aggregate risk, accounting for multiple events within a time frame. The VaR line represents the threshold below which losses are expected to remain for a specified probability, while the TVaR line provides an average loss value for scenarios that exceed this threshold. AEP curves are particularly important for portfolio-level risk management, allowing insurers to prepare for cumulative losses.
- OEP VaR and OEP TVaR: These curves display the risk associated with individual events. VaR indicates the expected maximum loss for a certain probability, while TVaR captures the average of the most severe outcomes. OEP metrics are essential for single-event scenarios, giving insight into high-impact incidents like a natural disaster or a major cyberattack.
Why EP Curves Matter for Insurers and Risk Managers
EP curves play a crucial role in strategic decision-making for insurers, enabling them to:
- Assess and Price Risk Accurately: By visualizing both frequent and rare loss scenarios, insurers can price their policies to reflect the true exposure, ensuring sustainability and profitability.
- Plan for Catastrophic Events: EP curves help insurers set aside sufficient reserves for worst-case scenarios, ensuring they’re prepared for extreme but low-probability events that could otherwise disrupt their financial stability.
- Optimize Reinsurance and Hedging Strategies: With an understanding of potential losses, insurers can structure their reinsurance contracts effectively, choosing coverage that aligns with their risk appetite. For example, they might select higher reinsurance limits if the EP curve indicates a significant tail risk.
- Inform Regulatory Compliance and Capital Requirements: Regulatory bodies often require insurers to demonstrate adequate capital reserves for catastrophic losses. EP curves provide the data-driven evidence needed to satisfy these requirements, proving that the insurer is adequately prepared for high-impact scenarios.
- Enhance Stakeholder Confidence: Transparency is key in the insurance industry. By leveraging EP curves, insurers can communicate their exposure, preparedness, and financial resilience to stakeholders, including regulators, investors, and clients.
Practical Applications: From Natural Disasters to Cyber Events
While EP curves were initially developed for natural catastrophe risks—such as hurricanes, earthquakes, and floods—they have now expanded into other domains. For example, in cyber insurance, EP curves can model the probability of significant financial loss from cyberattacks. With the rise of digital transformation, cyber risks are increasingly significant, and insurers rely on EP curves to quantify and manage these digital exposures.
Final Thoughts
The Exceedance Probability curve is more than just a statistical tool; it’s a powerful asset for any insurer managing catastrophe risks. Whether dealing with natural disasters or emerging threats like cyber risks, EP curves allow insurers to visualize and quantify risk, align their strategies, and strengthen financial resilience. By understanding and leveraging AEP, OEP, VaR, and TVaR metrics, insurers can make data-driven decisions to safeguard their portfolios, maintain regulatory compliance, and instill confidence in stakeholders.
In the high-stakes world of insurance, tools like EP curves are indispensable, providing clarity and foresight for navigating the unpredictable nature of catastrophic events. As new types of risks emerge, from climate change to cyber threats, the adaptability and insight offered by EP curves will continue to be invaluable in helping insurers stay one step ahead.

Head of catastrophe Modeling @Cyberwrite